6 - Effect Heterogeneity

Slides & Recap

Up until now, we have primarily discussed the general impact of a treatment. Let’s shift our focus to how treatments can affect different units in various ways. This involves the concept of personalized treatment effects and the improved assignment of treatments, especially in situations where it’s not feasible to treat everyone and prioritization is necessary. This topic is closely related to predictive problems, cross-validation, and model selection, with effect validation being more challenging than for a simple predictive model.

In recent weeks, we have occasionally estimated Conditional Average Treatment Effects (CATE) by manually assuming group-level heterogeneity.

\[ \tau(\mathbf{x}) = \mathbb{E}[Y_i(1) - Y_i(0) | \mathbf{X_i = x}] \]

Metalearners

Now predict individualized treatment effects based on all covariates \(X_i\) under the assumption of observed confounding using metalearners.

Tip

No proper cross-fitting

In the next steps, you are going to code the metalearners by hand. For simplicity, you don’t need to perform proper cross-fitting because the focus is on understanding the mechanisms of metalearners.

We will focus on the R-learner and the DR-learner, which have the advantage of minimizing only one loss function. However, there are also other types of metalearners, such as the S-learner, T-learner, and X-learner.

In general, metalearners combine multiple supervised machine learning steps into a pipeline that outputs predicted Conditional Average Treatment Effects (CATEs). The typical process involves:

  1. Estimating nuisance parameters.
  2. Plugging these estimates into a minimization problem targeting CATE.
  3. Solving the minimization problem.
  4. Using the model learned in step 3 to predict CATE.

R-learner

A robust and flexible approach to estimating heterogeneous treatment effects is the R-learner, which we will now examine. We will explore two specifications: the partially linear R-learner and the generic machine learning (ML) R-learner.

Partially linear R-learner

Related to the FWL theorem and the double machine learning with partially linear regression, which we discussed last time, the R-learner slightly adjusts the minimization problem by allowing the treatment effects to vary with the covariates \(mathbf{X}\).

\[ \underbrace{Y_i - \overbrace{\mathbb{E}[Y_i \mid \mathbf{X_i}]}^{\mu(\mathbf{X_i})}}_{\text{outcome residual}} = \tau(\mathbf{X_i}) \underbrace{( T_i - \overbrace{\mathbb{E}[T_i \mid \mathbf{X_i}]}^{e(\mathbf{X_i})})}_{\text{treatment residual}} + \epsilon_{Y_i} \] The minimization problem is the same except for the potentially heterogeneous treatment effect \(\tau(\mathbf{X_i})\) instead of the homogeneous treatment effect \(\tau)\).

\[ \hat{\tau}_{\text{RL}}(\mathbf{x}) = \arg \min_{\tau} \sum_{i=1}^n ( Y_i - \hat{\mu}(\mathbf{X_i}) - \tau(\mathbf{X_i}) ( T_i - \hat{e}(\mathbf{X_i})))^2 \] With some modifications, we can see that by using a modified covariate \(\mathbf{X_i}\), we can estimate with a linear model that minimize squares and solves the minimization problem in the final step.

\[ \begin{align*} \hat{\beta}_{RL} &= \underset{\beta}{\operatorname{arg\,min}} \sum_{i=1}^N( Y_i - \hat{\mu}(\mathbf{X_i}) - \mathbf{\beta'} \underbrace{(T_i - \hat{e}(\mathbf{X_i})) \mathbf{X_i}}_{=\mathbf{\tilde{X}_i}})^2 \\ &= \underset{\beta}{\operatorname{arg\,min}} \sum_{i=1}^N \left( Y_i - \hat{\mu}(\mathbf{X_i}) - \mathbf{\beta'} \mathbf{\tilde{X}_i} \right)^2 \end{align*} \] For estimating the outcome model \(\hat{\mu}(\mathbf{X_i})\) and the exposure model \(\hat{e}(\mathbf{X_i})\), we can use well suited ML functions.

Tip

Of course, there are packages and functions to just specify your data, treatment, outcome and covariates and you’ll get the result. But to better understand what’s going on under the hood, we are going to perform it manually here.

Imagine the following situation. You are operating an online shop, and a year ago, introduced a plus membership aimed at binding customers and driving revenue growth. The plus memberships comes at a small cost for the customers, which is why not all of the customers subscribed. Now you want to examine whether binding customers by this membership program in fact increases your sales with subscribed customers. However, it’s essential to consider potential confounding variables such as age, gender, or previous average purchase amounts. And this time you also measure a bunch of other variables which might let ML methods be more advantageous due to their way of handling high-dimensional data.

Each row in your dataset corresponds to a different customer, with accompanying demographic details, their average purchase sum before the introduction of the plus membership, their current average purchase, an indication of their participation in the plus membership program, and the categories they have bought in.

Warning: Paket 'ggplot2' wurde unter R Version 4.3.2 erstellt
Warning: Paket 'tidyr' wurde unter R Version 4.3.2 erstellt
membership <- readRDS("membership.rds")
glimpse(membership)
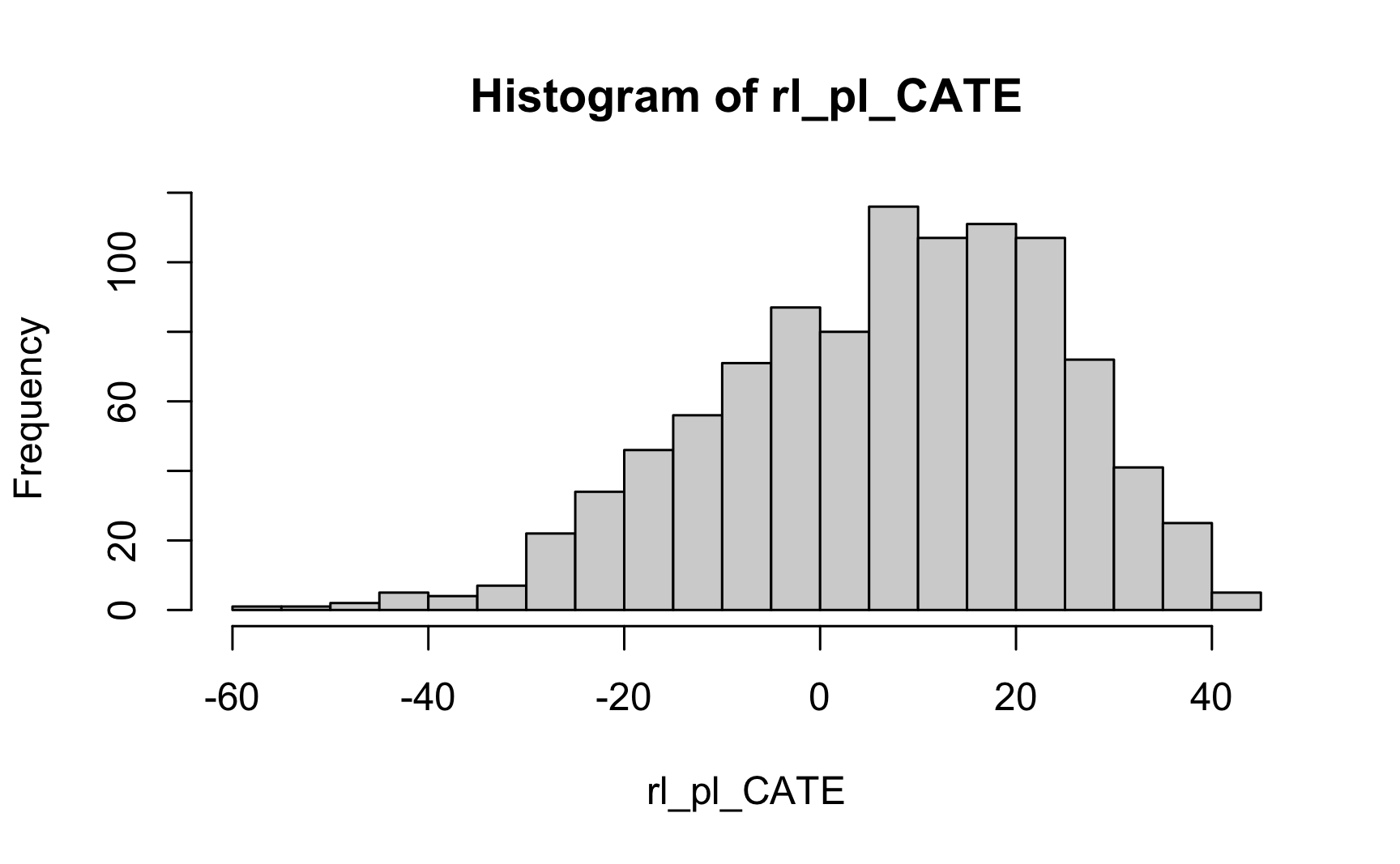
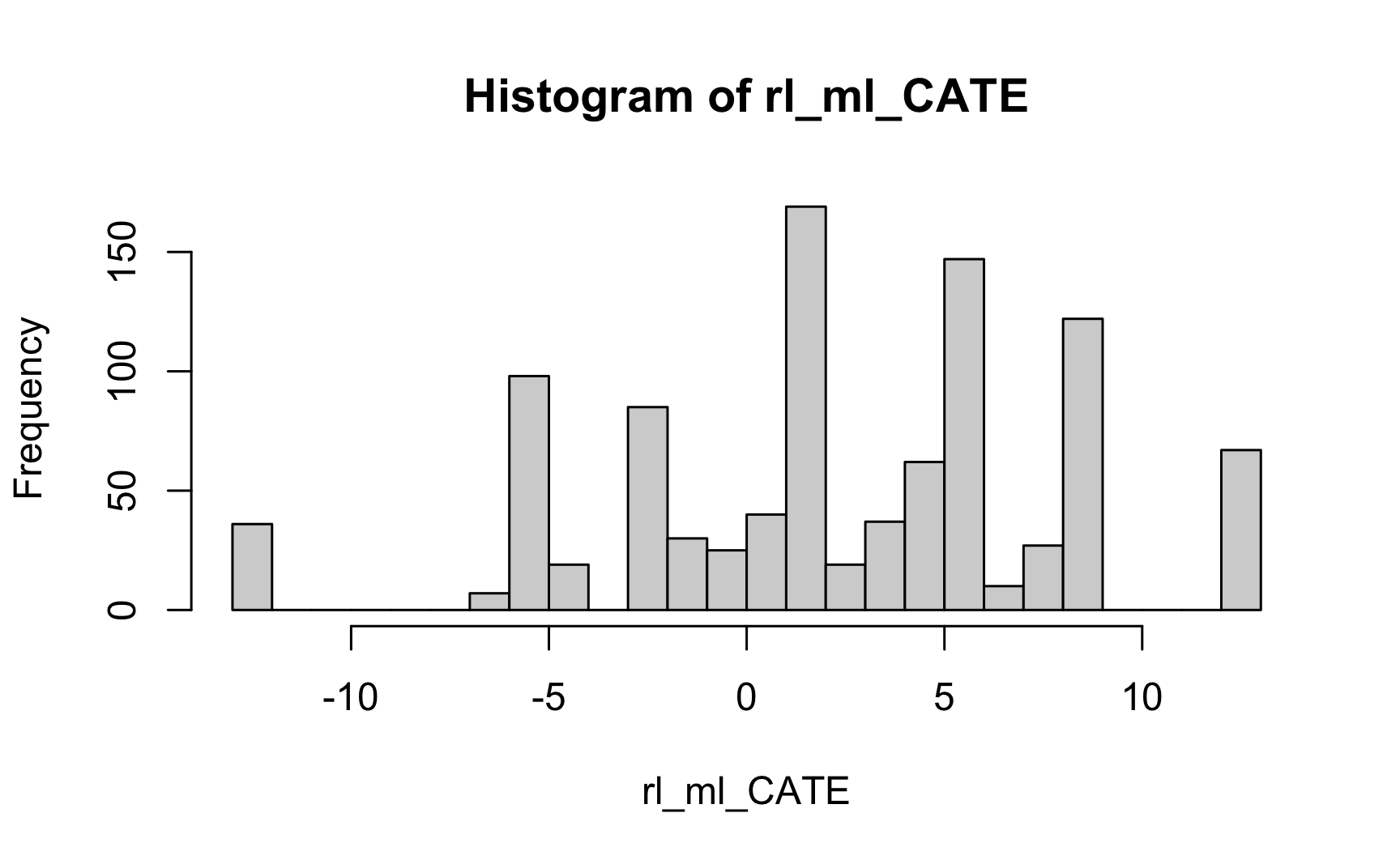
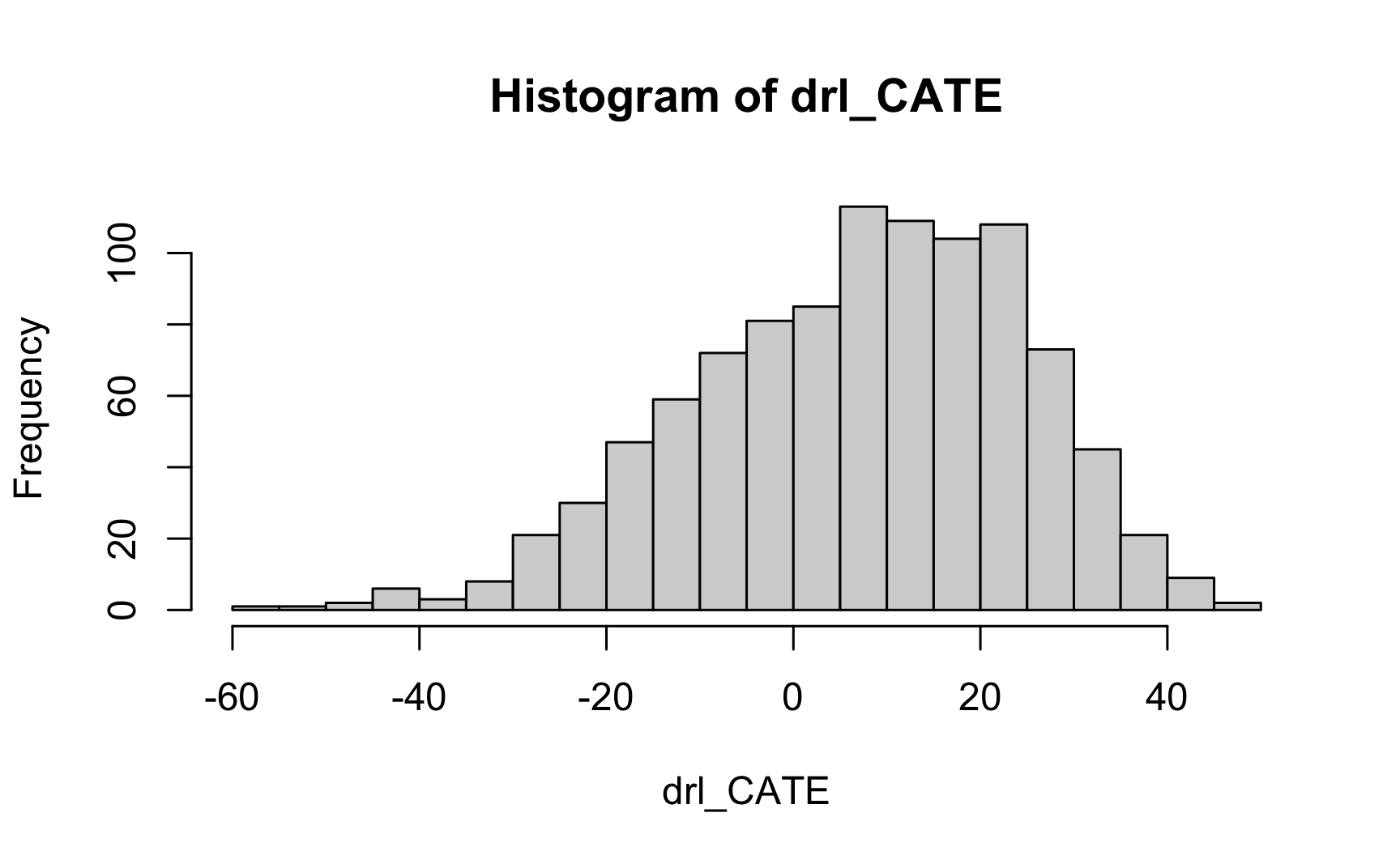
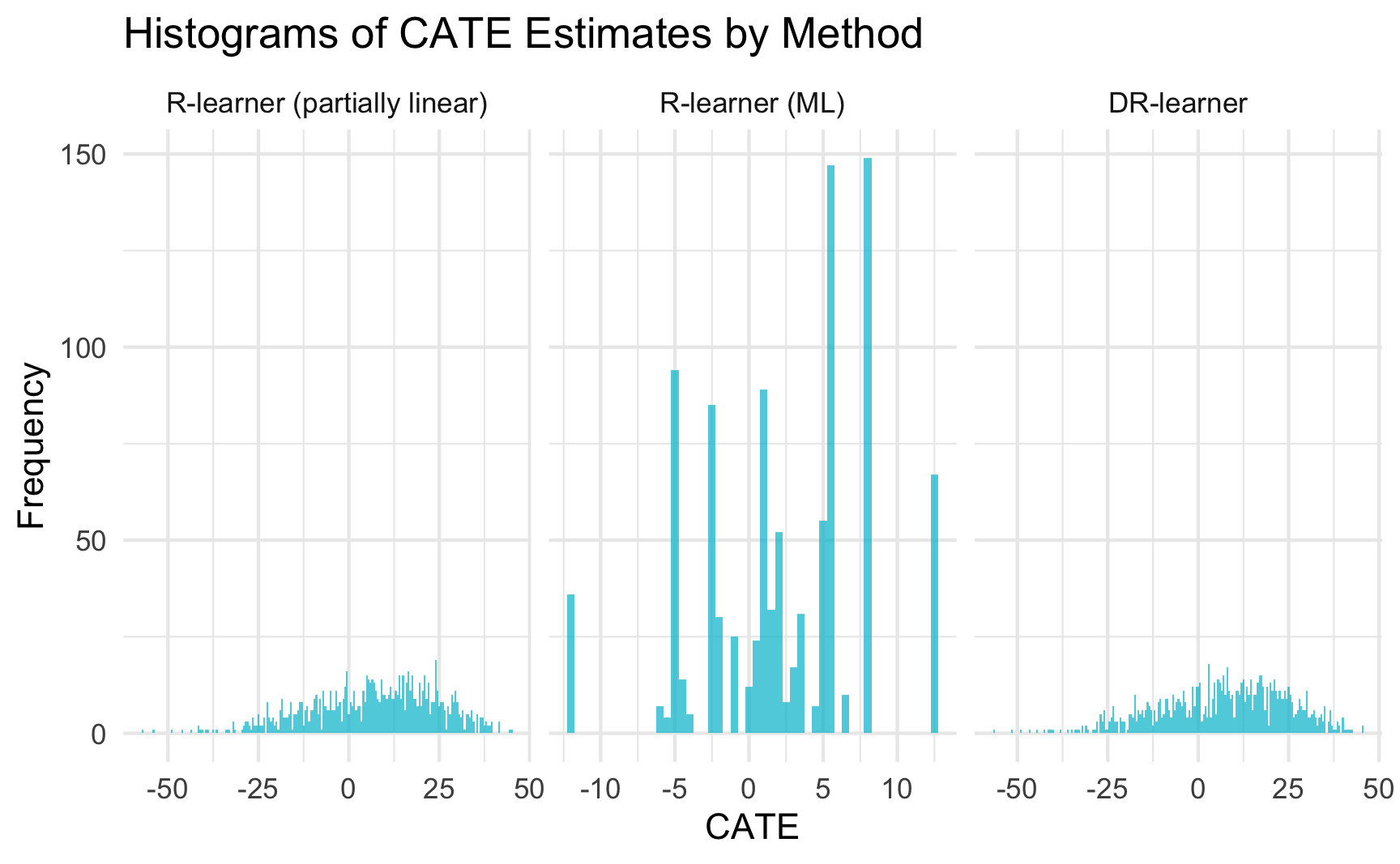
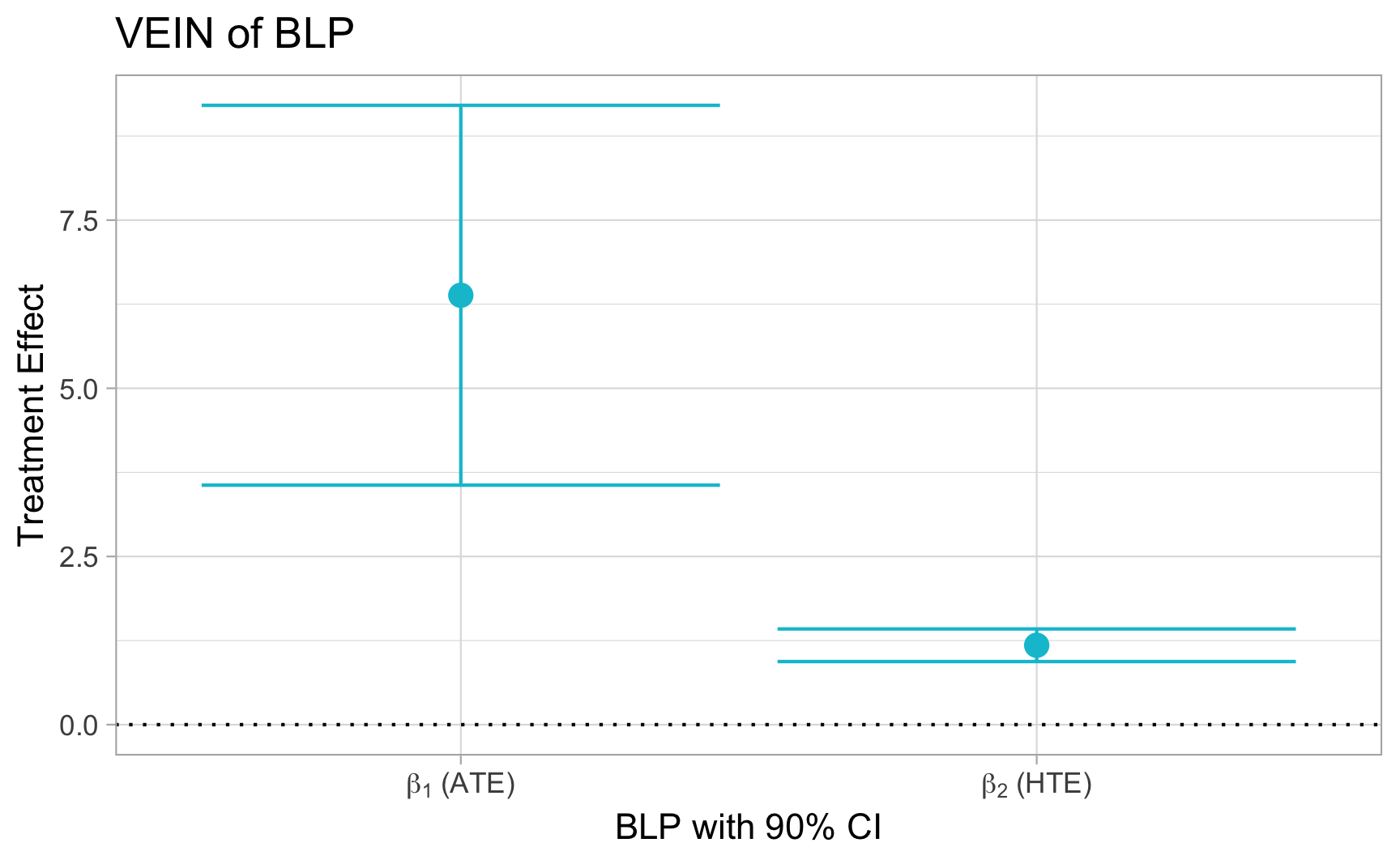
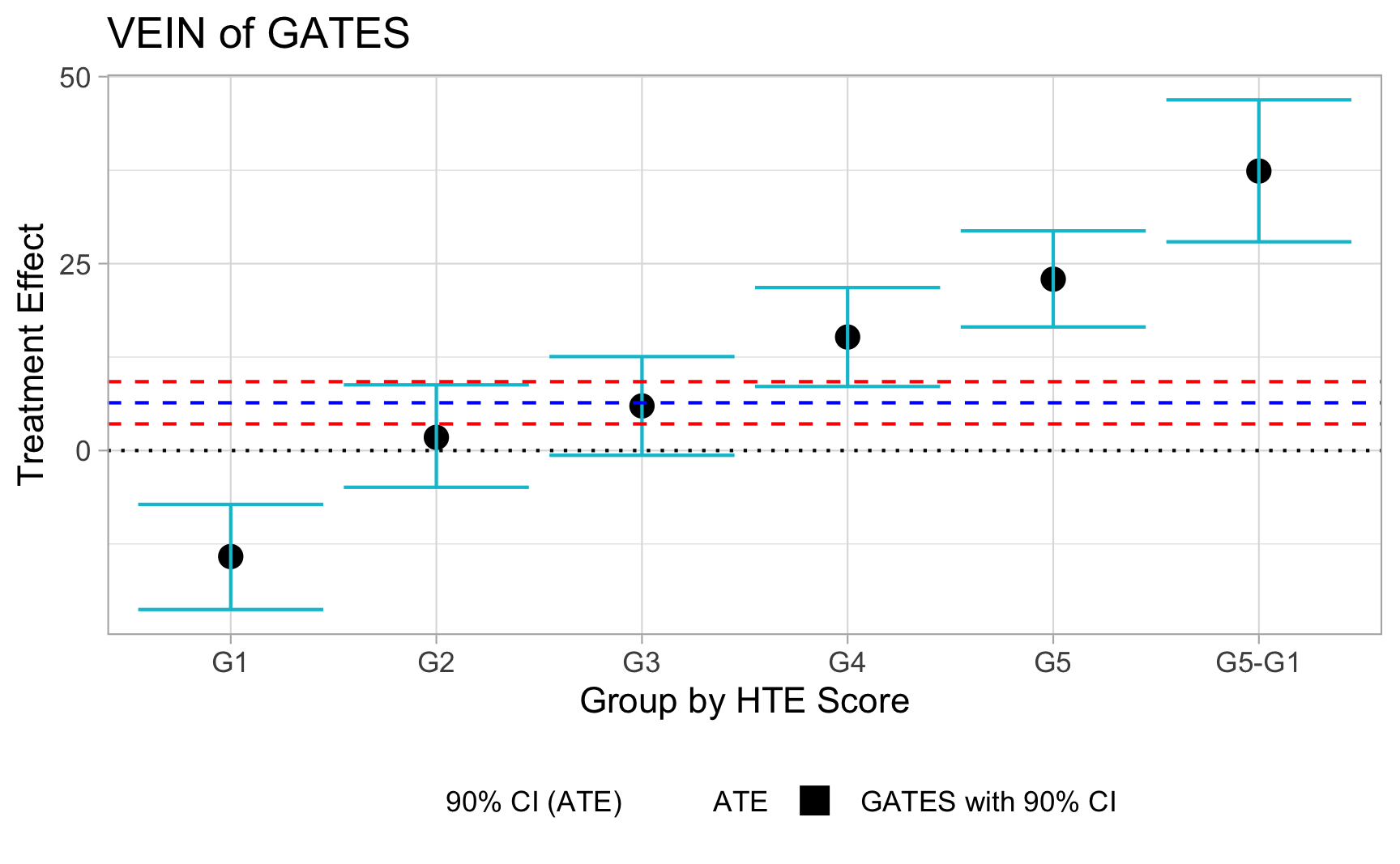
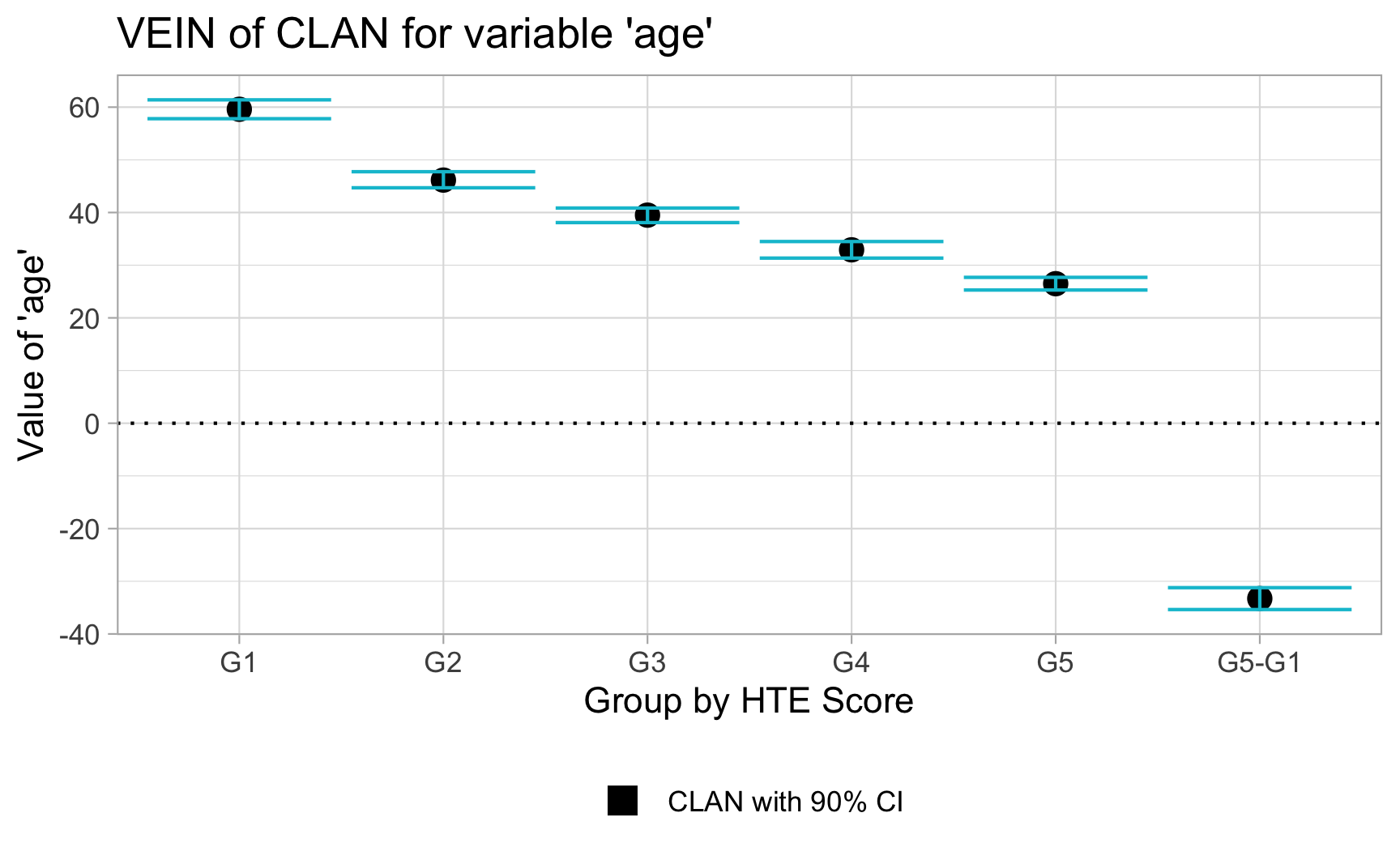
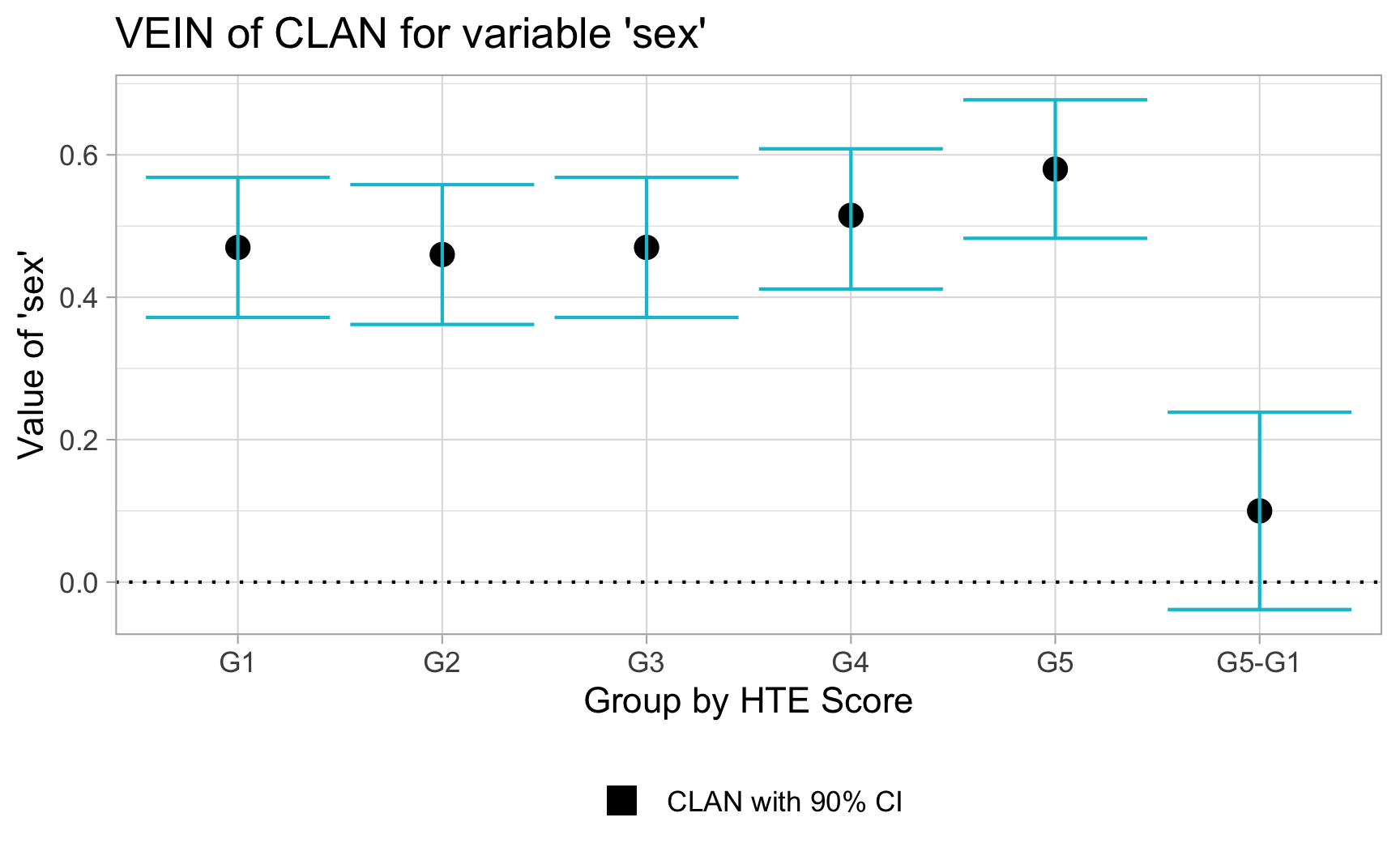
Rows: 1,000
Columns: 27
$ age                <dbl> 32, 42, 23, 67, 27, 54, 40, 27, 29, 35, 22, 37, 25, 41, 37, 60, 32, 31, 30, 41, 34, 48, 42, 41, 38, 29, 37, 27, 26, 27, 5…
$ sex                <int> 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0…
$ pre_avg_purch      <dbl> 22, 32, 32, 47, 30, 31, 38, 26, 26, 47, 36, 55, 32, 26, 48, 41, 23, 23, 33, 30, 31, 25, 43, 37, 22, 40, 33, 24, 23, 37, 3…
$ card               <int> 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1…
$ avg_purch          <dbl> 45.45, 72.73, 64.20, 55.66, 80.08, 35.34, 10.22, 45.32, 0.56, 69.84, 53.71, 55.46, 53.50, 44.00, 29.72, 33.08, 32.08, 37.…
$ vehicle            <int> 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
$ food               <int> 1, 2, 0, 1, 1, 0, 1, 0, 0, 0, 2, 0, 1, 2, 1, 0, 0, 1, 1, 2, 1, 2, 4, 1, 0, 2, 2, 0, 0, 2, 1, 2, 2, 2, 2, 2, 1, 0, 1, 1, 1…
$ beverage           <int> 2, 2, 2, 2, 0, 0, 0, 0, 0, 0, 0, 1, 2, 1, 0, 3, 0, 0, 1, 0, 1, 4, 0, 2, 3, 1, 1, 2, 2, 1, 1, 1, 1, 2, 0, 1, 1, 0, 2, 1, 0…
$ art                <int> 0, 2, 1, 2, 1, 0, 0, 1, 1, 1, 3, 0, 0, 3, 1, 3, 1, 0, 0, 0, 2, 1, 2, 1, 1, 1, 1, 0, 1, 2, 3, 0, 2, 0, 2, 0, 1, 0, 1, 2, 0…
$ baby               <int> 1, 1, 1, 1, 1, 1, 2, 1, 3, 1, 2, 0, 1, 2, 0, 0, 0, 2, 0, 0, 0, 1, 0, 1, 2, 2, 3, 1, 1, 0, 1, 2, 0, 2, 0, 0, 2, 2, 0, 1, 1…
$ personal_care      <int> 0, 0, 2, 1, 1, 1, 3, 1, 1, 0, 1, 1, 0, 0, 1, 0, 2, 0, 1, 1, 0, 1, 2, 1, 0, 2, 0, 0, 3, 2, 1, 1, 1, 2, 0, 1, 0, 3, 1, 2, 1…
$ toys               <int> 0, 0, 3, 2, 1, 1, 1, 2, 2, 0, 0, 1, 2, 3, 0, 1, 1, 0, 1, 2, 1, 0, 1, 0, 1, 0, 0, 0, 2, 0, 1, 2, 3, 0, 1, 0, 1, 1, 1, 1, 1…
$ clothing           <int> 2, 1, 2, 2, 2, 1, 1, 2, 2, 2, 5, 1, 1, 1, 1, 3, 0, 1, 2, 2, 5, 2, 3, 1, 2, 1, 1, 0, 0, 1, 0, 0, 2, 5, 1, 0, 3, 1, 1, 2, 1…
$ decor              <int> 0, 0, 0, 3, 2, 2, 0, 1, 1, 0, 2, 0, 0, 2, 1, 1, 0, 1, 0, 2, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 3, 1, 2, 2, 2, 0, 0, 1, 1, 2…
$ cell_phones        <int> 1, 2, 4, 1, 1, 2, 4, 4, 3, 1, 5, 1, 3, 2, 3, 4, 3, 3, 1, 4, 3, 5, 2, 4, 5, 5, 5, 4, 2, 4, 2, 2, 2, 3, 5, 3, 3, 2, 3, 4, 1…
$ construction       <int> 1, 2, 1, 1, 1, 4, 1, 0, 3, 0, 0, 0, 2, 1, 0, 0, 2, 0, 0, 0, 1, 2, 1, 2, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 3, 1, 2, 1, 1, 3…
$ home_appliances    <int> 0, 2, 0, 1, 1, 0, 1, 0, 0, 2, 1, 0, 0, 0, 2, 0, 1, 1, 1, 2, 0, 1, 0, 1, 1, 0, 2, 0, 3, 0, 1, 4, 1, 1, 1, 0, 1, 2, 1, 2, 2…
$ electronics        <int> 1, 2, 4, 0, 2, 2, 1, 2, 2, 3, 1, 3, 3, 0, 4, 1, 2, 1, 2, 2, 2, 0, 2, 2, 0, 2, 4, 0, 0, 2, 4, 2, 2, 1, 0, 2, 1, 1, 0, 3, 2…
$ sports             <int> 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 2, 4, 0, 2, 0, 3, 2, 0, 1, 0, 1, 2, 3, 4, 0, 2, 1, 1, 0, 1, 0, 1, 2…
$ tools              <int> 3, 2, 1, 1, 1, 2, 1, 0, 4, 2, 1, 0, 0, 2, 0, 1, 1, 2, 2, 0, 0, 1, 1, 0, 0, 0, 0, 2, 1, 0, 1, 0, 3, 0, 0, 1, 0, 2, 1, 0, 0…
$ games              <int> 4, 1, 3, 1, 2, 1, 3, 1, 0, 3, 0, 1, 1, 7, 1, 3, 0, 1, 2, 3, 0, 2, 2, 1, 2, 6, 3, 1, 2, 1, 0, 2, 2, 2, 2, 2, 2, 3, 2, 2, 2…
$ industry           <int> 0, 0, 2, 0, 0, 1, 0, 0, 3, 2, 1, 2, 1, 0, 0, 2, 1, 0, 3, 0, 0, 0, 3, 1, 3, 0, 1, 3, 2, 0, 2, 0, 2, 1, 1, 0, 0, 2, 0, 2, 1…
$ pc                 <int> 4, 2, 2, 2, 3, 0, 2, 1, 3, 0, 3, 2, 3, 3, 2, 1, 0, 0, 3, 2, 3, 2, 1, 1, 3, 1, 3, 2, 2, 0, 2, 4, 2, 1, 0, 0, 4, 2, 3, 2, 0…
$ jewel              <int> 0, 1, 0, 0, 0, 2, 0, 0, 0, 4, 1, 0, 0, 1, 3, 1, 0, 3, 1, 4, 0, 1, 2, 0, 1, 2, 2, 2, 2, 0, 1, 1, 0, 2, 0, 0, 1, 4, 0, 1, 1…
$ books              <int> 2, 1, 0, 0, 1, 0, 0, 0, 4, 2, 1, 2, 1, 2, 0, 1, 0, 0, 0, 3, 0, 3, 1, 2, 2, 2, 2, 1, 0, 1, 2, 1, 1, 1, 1, 0, 0, 3, 0, 2, 1…
$ music_books_movies <int> 1, 3, 3, 2, 2, 1, 1, 0, 2, 2, 0, 0, 2, 3, 2, 0, 1, 0, 2, 1, 0, 1, 2, 1, 1, 0, 0, 1, 2, 0, 1, 0, 2, 0, 2, 1, 2, 0, 1, 0, 0…
$ health             <int> 0, 0, 2, 2, 6, 0, 4, 2, 2, 2, 2, 0, 3, 1, 0, 2, 3, 2, 1, 3, 4, 2, 3, 1, 2, 1, 5, 3, 2, 2, 5, 1, 5, 2, 1, 0, 0, 4, 5, 4, 3…

Again, we are going to rely on the mlr3 packages for ML models.

# Load packages
library(mlr3)
library(mlr3learners)

In the first step, we train the models for the nuisance parameters \(\hat{\mu}(\mathbf{X_i})\) and \(\hat{e}(\mathbf{X_i})\).

Q1: Specify the nuisance models. Then, train and predict to obtain the residuals.

Code
## Specify
# Prediction model for the treatment/exposure
task_e <- as_task_classif(membership |> select(-avg_purch), target = "card")
lrnr_e <- lrn("classif.log_reg", predict_type = "prob")

# Prediction model for the outcome
task_m <- as_task_regr(membership |> select(-card), target = "avg_purch")
lrnr_m <- lrn("regr.lm")

## Train
lrnr_m$train(task_m)
lrnr_e$train(task_e)

## Predict
m_pred_tbl <- lrnr_m$predict(task_m)
e_pred_tbl <- lrnr_e$predict(task_e)

## Residualize
# True values
D <- membership$card
Y <- membership$avg_purch

# Residuals
Y_res <- Y - m_pred_tbl$response
D_res <- D - e_pred_tbl$prob[, 2]

Now, you can construct the modified covariates as obtained in the minimization problem.

\[ \mathbf{\tilde{X}_i} = (T_i - \hat{e}(\mathbf{X_i})) \mathbf{X_i} \] Please note, that you also have to include the intercept column with all values equal to 1, e.g. by using rep(1, n) or mutate(intercept = 1).

Q2: Construct a data frame or matrix that contains the modified covariates and the intercept.

Code
# Get matrix of unmodified covariates
X <- membership |> select(-avg_purch, -card) |> mutate(intercept = 1)
X <- as.matrix(X)

# Modify by multiplying with residuals
X_tilde <- X * D_res

Now, you need to solve the minimization problem. Since we are focusing on a linear model, you can use the lm() function. Alternatively, you can apply linear shrinkage estimators, such as Lasso.

Q3: Run a regression of the residualized outcome on the modified covariates and report the results.

Code
# Partially linear R-Learner
rl_pl <- lm(Y_res ~ 0 + X_tilde)
summary(rl_pl)

Call:
lm(formula = Y_res ~ 0 + X_tilde)

Residuals:
   Min     1Q Median     3Q    Max 
-46.41 -10.92   0.22  10.49  39.31 

Coefficients:
                          Estimate Std. Error t value Pr(>|t|)    
X_tildeage                 -1.1424     0.0842  -13.56  < 2e-16 ***
X_tildesex                  6.6572     1.9958    3.34  0.00088 ***
X_tildepre_avg_purch       -0.1253     0.1014   -1.24  0.21698    
X_tildevehicle              0.5023     3.2101    0.16  0.87568    
X_tildefood                -0.5471     1.0029   -0.55  0.58550    
X_tildebeverage            -0.2443     1.0019   -0.24  0.80743    
X_tildeart                  0.7067     0.9858    0.72  0.47365    
X_tildebaby                -0.9090     1.0073   -0.90  0.36707    
X_tildepersonal_care       -1.1645     0.9598   -1.21  0.22533    
X_tildetoys                 1.2214     0.9722    1.26  0.20928    
X_tildeclothing            -0.0405     0.7201   -0.06  0.95517    
X_tildedecor                0.6599     0.9482    0.70  0.48663    
X_tildecell_phones         -0.1243     0.5666   -0.22  0.82637    
X_tildeconstruction         0.2585     0.9667    0.27  0.78921    
X_tildehome_appliances      0.3960     1.0720    0.37  0.71192    
X_tildeelectronics         -0.2746     0.6926   -0.40  0.69184    
X_tildesports              -0.1140     0.9825   -0.12  0.90769    
X_tildetools               -0.9351     1.0366   -0.90  0.36723    
X_tildegames               -0.4941     0.6857   -0.72  0.47133    
X_tildeindustry             0.8194     1.0548    0.78  0.43744    
X_tildepc                   1.1932     0.7115    1.68  0.09384 .  
X_tildejewel                0.8425     0.9792    0.86  0.38978    
X_tildebooks               -0.3454     0.9799   -0.35  0.72454    
X_tildemusic_books_movies   0.9734     0.9791    0.99  0.32035    
X_tildehealth               0.4330     0.7162    0.60  0.54560    
X_tildeintercept           52.0186     6.3475    8.20  7.8e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 15 on 974 degrees of freedom
Multiple R-squared:  0.26,  Adjusted R-squared:  0.24 
F-statistic: 13.1 on 26 and 974 DF,  p-value: <2e-16

Having trained the model, you obtain coefficients which you can multiply with \(\mathbf{X}\) (not \(\mathbf{\tilde{X}}\)) to get the \(CATE\).

Note

Matrix multiplication in R is done using mn %*% nm. Make sure to use the correct order.

\[ \hat{\tau}_{\text{RL}}(\mathbf{x}) = \mathbf{\hat{\beta}_{RL} x} \neq \mathbf{\hat{\beta}_{RL} \tilde{x}} \]

Q4: Get the predicted conditional average treatment effects CATE.

Code
# Multiply covariates with coefficient vector
rl_pl_CATE <- X %*% rl_pl$coefficients
hist(rl_pl_CATE, breaks = 30)

Generic ML R-learner

In the previous estimation, we imposed linearity on the CATE. However, sometimes you might not want to assume linearity. By rearranging the minimization problem, you can see that you can use any machine learning method capable of handling weighted minimization.

$$ \[\begin{align*} \hat{\tau}_{\text{RL}}(\mathbf{x}) &= \arg \min_{\tau} \sum_{i=1}^n ( Y_i - \hat{\mu}(\mathbf{X_i}) - \tau(\mathbf{X_i}) ( T_i - \hat{e}(\mathbf{X_i})))^2 \\ &= ... \\ &= \arg \min_{\tau} \sum_{i=1}^n (T_i - \hat{e}(\mathbf{X_i}))^2 \bigg(\frac{Y_i - \hat{\mu}(\mathbf{X_i})}{ T_i - \hat{e}(\mathbf{X_i})} - \tau(\mathbf{X_i})\bigg)^2 \\ \end{align*}\] $$

The estimation procedure again requires the outcome and treatment model estimated as a first step to obtain residuals. Then, however, you proceed with the

  1. weights

\[ (T_i - \hat{e}(\mathbf{X_i}))^2, \]

  1. a pseudo-outcome

\[\frac{Y_i - \hat{\mu}(\mathbf{X_i})}{ T_i - \hat{e}(\mathbf{X_i})}\] and 3. unmodified covariates \(X\).

Q5: Construct the weights and the pseudo-outcome.

Code
# Pseudo - outcome
Y_pseudo_rl <- Y_res / D_res

# Weight
weight_rl <- D_res^2

# Add pseudo-outcome, weights and unmodified covariates to a matrix/data frame
data_rl <- cbind(X, Y_pseudo_rl, weight_rl)
Tip

Hints: ML methods capable of performing weighted minimization are e.g. lrn("regr.xgboost") or lrn("regr.randomForest"). To specify the weight, you can use: task_rl$set_col_roles(col = "weight_rl", roles = "weight").

Q6: Specify a ML method capable of performing weighted minimization. Then, train and predict.

Code
## Specify task and learner
# Task
task_rl <- as_task_regr(data_rl, target = "Y_pseudo_rl")
# Assign weight column
task_rl$set_col_roles(col = "weight_rl", roles = "weight")

# Specify learner
lrnr_rl <- lrn("regr.xgboost")

# Train
lrnr_rl$train(task_rl)

# Predict CATEs
rl_ml_CATE <- lrnr_rl$predict(task_rl)$response
hist(rl_ml_CATE, breaks = 30)

DR-learner

The doubly robust learner we discussed in the previous chapter is also a metalearner we can exploit to estimate heterogeneous effects.

\[ \tau_{\text{DR}}(\mathbf{x}) = \mathbb{E}\bigg[ \underbrace{\hat{\mu}(1, \mathbf{X_i}) - \hat{\mu}(0, \mathbf{X_i}) + \frac{T_i(Y_i - \hat{\mu}(1, \mathbf{X_i}))}{ \hat{e}_1(\mathbf{X_i})} - \frac{(1-T_i)(Y_i - \hat{\mu}(0, \mathbf{X_i})}{\hat{e}_0(\mathbf{X_i}))}}_{\tilde{\tau_i}_{\text{ATE}}^{\text{AIPW}}} \bigg| \mathbf{X_i= x} \bigg] \]

You might remember that we predicted both potential outcomes and obtained estimates of the individual treatment effect.

\[ \tau_{\text{DR}}(\mathbf{x}) = \mathbb{E}\bigg[ \tilde{\tau_i}_{\text{ATE}}^{\text{AIPW}} \bigg| \mathbf{X_i= x} \bigg] \]

The only step left is then to regress these estimates on the assumed drivers of heterogeneity in effects.

\[ \hat{\tau}_{RL}(\mathbf{x}) = \underset{\tau}{\operatorname{arg\,min}} \sum_{i=1}^N \left( \tilde{\tau_i}_{\text{ATE}}^{\text{AIPW}} - \tau(\mathbf{X_i})\right)^2 \]

Q7: Specify your nuisance parameters. Then, train and predict to obtain m0_hat, m1_hat and e_hat.

Code
## Train outcome models
# Y0 ~ X
lrnr_m$train(task_m, row_ids = which(membership$card == 0))
m0_hat <- lrnr_m$predict(task_m)$response

# Y1 ~ X
lrnr_m$train(task_m, row_ids = which(membership$card == 1))
m1_hat <- lrnr_m$predict(task_m)$response

# D ~ X (already trained)
e_hat <- e_pred_tbl$prob[, 2]

Q8: Construct the pseudo-outcome used to compute the ATE \({\text{ATE}}^{\text{AIPW}}\). Regress it on \(X\) and obtain the fitted values.

Code
# Pseudo-outcome
tau_dr <- m1_hat - m0_hat + D * (Y - m1_hat) / e_hat - (1 - D) * (Y - m0_hat) / (1-e_hat)

# Fit regression
drl_mod <- lm(tau_dr ~ 0 + X)
# "Predict"
drl_CATE <- drl_mod$fitted.values

# Plot histogram
hist(drl_CATE, breaks = 30)

Comparison

# Store and plot predictions
results <- tibble(
  "R-learner (partially linear)" = rl_pl_CATE,
  "R-learner (ML)" = rl_ml_CATE,
  "DR-learner" = drl_CATE
  )
# Correlation of CATEs by different methods
cor(results, method = "pearson")
                             R-learner (partially linear) R-learner (ML) DR-learner
R-learner (partially linear)                          1.0            0.8        1.0
R-learner (ML)                                        0.8            1.0        0.8
DR-learner                                            1.0            0.8        1.0
# Summary statistics
summary(results)
 R-learner (partially linear).V1 R-learner (ML)    DR-learner 
 Min.   :-57                     Min.   :-12.2   Min.   :-57  
 1st Qu.: -5                     1st Qu.: -2.0   1st Qu.: -5  
 Median :  8                     Median :  1.9   Median :  8  
 Mean   :  7                     Mean   :  2.3   Mean   :  7  
 3rd Qu.: 20                     3rd Qu.:  5.7   3rd Qu.: 20  
 Max.   : 45                     Max.   : 12.4   Max.   : 46
Code
# Reshape data to long format
results_long <- results %>%
  pivot_longer(cols = everything(), names_to = "Method", values_to = "Value") |> 
  mutate(Method = factor(Method, levels = c("R-learner (partially linear)", "R-learner (ML)", "DR-learner")))

# Create the histograms
ggplot(results_long, aes(x = Value)) +
  geom_histogram(binwidth = 0.5, alpha = 0.75) + # Adjust binwidth as needed
  facet_wrap(~ Method, scales = "free_x") +
  theme_minimal() +
  labs(title = "Histograms of CATE Estimates by Method",
       x = "CATE",
       y = "Frequency")

Evaluation of effect heterogeneity

While we have learned to estimate the CATE and observe variation in the estimated individual response to the treatment, we have not yet determined whether this heterogeneity is systematic or merely noise. Evaluating our estimated CATEs is challenging because we cannot use the typical out-of-sample approach due to the missing counterfactual. Additionally, using ML methods in the final step provides no statistical inference.

To address this, we can derive summary statistics for the distribution of CATEs and jointly test for the presence of heterogeneity and our ability to detect it. Three methods we will explore are:

  • BLP: Best Linear Predictor
  • GATES: High-vs-low Sorted Group Average Treatment Effect
  • CLAN: Classification Analysis

For the further analysis, we will rely on the GenericML package, which provides the functions get_BLP(), get_GATES() and getCLAN() which we can apply on a GenericML object.

install.packages("GenericML")
# Load package
library(GenericML)

It also builds upon the mlr3 package and we can again specify our learners. Here, we can also specify more than one learner and let GenericML figure out which one performs best.

# Specify set of learners
lrnr <- c("mlr3::lrn('svm')", 'mlr3::lrn("ranger", num.trees = 100)')

ADD good explanation

# Specify covariates to use
X1 <- setup_X1(funs_Z = c("S", "B", "p"))
Note

You might get a warning saying that some of your propensity scores are outside the interval [0.35, 0.65]. Generally, it is only recommended to use the package when having randomized data. For the sake of demonstration, we will ignore the warning here.

gen_ML <- GenericML(
  # data
  Z = X, 
  D = D,
  Y = Y,
  # learners
  learners_GenericML = lrnr,
  learner_propensity_score = "lasso",
  # algorithm
  num_splits = 10,
  quantile_cutoffs = c(0.2, 0.4, 0.6, 0.8),
  # regression setup
  X1_BLP = X1,
  X1_GATES = X1,
  # computational issues
  parallel = TRUE, 
  num_cores = 6, 
  seed = 11
)

Best linear predictor

First, we take a look at the best linear predictor (BLP). It aims to provide the solution of the hypothetical regression of the true CATE on the demeaned predicted CATE. Thereby, it attempts to answer whether heterogeneity is present and we are able to detect it. It is a straightforward way to check the quality of our predictions.

\[ \mathbb{E}[\tau(\mathbf{X_i}) | \hat{\tau}(\mathbf{X_i}) ] := \beta_1 + \beta_2\underbrace{(\hat{\tau}(\mathbf{X_i}) - \mathbb{E}[\hat{\tau}(\mathbf{X_i})])}_{\text{demeaned prediction}} \] Because we do not know the actual true treatment effect, we use a pseudo-response that we regress on the demeaned CATE.

Using GenericML, we just have to run:

get_BLP(gen_ML, plot = TRUE)
BLP generic targets
---
       Estimate CI lower CI upper p value
beta.1    6.383    3.560    9.206       0
beta.2    1.180    0.938    1.423       0
---
Confidence level of confidence interval [CI lower, CI upper]: 90 %

Question: What does \(\beta_1\) represent?

Question: What does \(\beta_2\) represent? What, if \(\beta_2 = 0\)?

Sorted group average treatment effects

Sorted group average treatment effects (GATES) offers insights into the distribution and heterogeneity of treatment effects. The procedure involves sorting and slicing the distribution of the predicted treatment effects \(\hat{\tau}(\mathbf{X_i})\) into \(K\) parts and then compute \(ATE\)s for each of the slices. When these slices are different from each other, we can identify subgroups which response differently to the treatment.

Mathematically, we ran

\[ \gamma_k := \mathbb{E}[ \tau(\mathbf{X_i}) | G_k]. \]

When the estimator approximates well, we expect to see monotonicity in estimates:

\[ \gamma_1 \leq \gamma_2 \leq \ldots \leq \gamma_K \] Using GenericML, we just have to run:

get_GATES(gen_ML, plot = TRUE)
GATES generic targets
---
                Estimate CI lower CI upper p value
gamma.1          -14.179  -21.268   -7.208    0.00
gamma.2            1.759   -4.916    8.786    0.55
gamma.3            5.966   -0.635   12.567    0.04
gamma.4           15.179    8.566   21.791    0.00
gamma.5           22.919   16.526   29.377    0.00
gamma.5-gamma.1   37.383   27.915   46.900    0.00
---
Confidence level of confidence interval [CI lower, CI upper]: 90 %

Question: Discuss the output. Do you see the assumed monotonicity in the estimates?

Classification analysis

The purpose of classification analysis (CLAN) is to explore what drives the heterogeneous effects. Instead of regressing a pseudo-outcome as in GATES, covariates, which are potential drivers of heterogeneity in treatment effect are regressed upon. In other words, CLAN is a simple mean comparison of covariates in groups split by the size of their treatment effect.

get_CLAN(gen_ML, variable = "age", plot = TRUE)
CLAN generic targets for variable 'age' 
---
                Estimate CI lower CI upper p value
delta.1             59.6     57.8     61.4       0
delta.2             46.2     44.7     47.7       0
delta.3             39.5     38.1     40.8       0
delta.4             32.9     31.3     34.5       0
delta.5             26.5     25.3     27.7       0
delta.5-delta.1    -33.3    -35.4    -31.2       0
---
Confidence level of confidence interval [CI lower, CI upper]: 90 %

get_CLAN(gen_ML, variable = "sex", plot = TRUE)
CLAN generic targets for variable 'sex' 
---
                Estimate CI lower CI upper p value
delta.1           0.4700   0.3717   0.5683    0.00
delta.2           0.4600   0.3618   0.5582    0.00
delta.3           0.4700   0.3717   0.5683    0.00
delta.4           0.5150   0.4115   0.6085    0.00
delta.5           0.5800   0.4828   0.6772    0.00
delta.5-delta.1   0.1000  -0.0386   0.2386    0.12
---
Confidence level of confidence interval [CI lower, CI upper]: 90 %

Question: Interpret the plots.

Assignment

Coming soon.

Accept the Week 6 - Assignment and follow the same steps as last week and as described in the organization chapter.

For the assignments you are going to use music.rds. Consider the following scenario: you are a data scientist at a music streaming company. Naturally, you’re keen to engage users for as long as possible and encourage them to become avid users of your streaming app. Your colleagues from the department responsible for recommendation algorithms have developed a new fancy algorithm which aims to enhance the daily number of minutes of music listening by offering particularly well tailored recommendations. Following common practice of A/B testing, you randomly assign your users into a treatment group (new algorithm) and a control group (no new algorithm). The outcome variable is minutes_spent and the treatment variable is new_algo.

  1. As you’ve learned, in an A/B test you just need to regress the outcome on the treatment. Follow that and interpret the estimated ATE.

  2. Take a look at the two formula rearrangements for the R-learner. For both approaches, construct the predicted treatment effects and coefficients and show the equivalence. (You don’t need to use cross-fitting)

  3. Using the DoubleML package, run the DR-learner and check for CATEs based on your available covariates. Do you find heterogeneous treatment effects? If yes, interpret them (also with regard to your coefficient in the first task). Please note that to extract the doubly robust \(\tilde{\tau_i}_{\text{ATE}}\), you need to access dr_mod$psi_b.

  4. For the covariate app_usage_frequency, use the package np to check for non-linear heterogeneous treatment effects. Check lecture slide 12 for more details. Discuss the result.